2021年 令和３年 宅建 合格点は33点 34点と予想しました④

ひかるオープンチャットのメンバーから、宅建資格予備校大手C社の2019年と2021年の本試験の結果が入手できましたので分析してみます

C社の本試験の得点別人数分布の予想

③のブログにて、予備校が行うと思われる合格点予想について説明しました

当然のことながら、各予備校は、自社の企業秘密である、自校生の得点分布を公開することはありません。

そこで、実際のデータとは誤差が生じることを覚悟の上で、限られたデータを用いて、得点と人数分布が正規分布になっているとの前提で分析を行うこととしました

ただ、予備校や講師のみなさんも、実データを用いて、合格点を求めるときは、35点は〇〇％、34点は△△％と表を見ながら合格ラインを決めるのではなく、一度、データを統計処理し、確率分布から各得点ごとの合格確率を求めるこをやった方が、いいと思います（公表がないので、やってないと勝手に思っていますが、やっていたらごめんなさい！）

◇

さて、C社の生徒は、自分の本試験の結果を登録すると、各自の成績表をもらいますが、その中には

のデータが掲載されています

これだけあれば、正規分布を描くことができます。ひかるオープンチャットのメンバーAさんから情報をいただきました、データ的にはこんな感じです（Aさんの数値ではありません）

C社の通学生の成績です

ちなみ、

2019年の本試験
合格点35点　合格率17.0%

です

正規分布

正規分布とは、

式はこれです！！

ｘ：得点、f(x)：得点ｘが発生する確率、μ：平均値、σ：標準偏差

になります

◇

え？難しすぎてわからない？

じゃあ、簡単に説明しましょう。

宅建のような大規模な試験をした場合、得点と人数の分布は、だいたい、このようなグラフになることが統計学では知られています。興味のある方は、まずこちらを大読みください

大体、こんな感じです

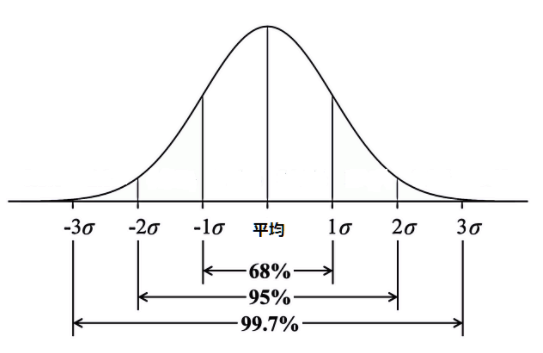
横軸は得点、縦軸は人数または割合と思ってください

でも、宅建の試験の分布って、こんな分布になりますか？そこは大丈夫です。今回やりたいのは2019年と2021年の相対比較なので、多少、山が変形していても、母集団＝C社の通学生の分布が同じなら、結果を導き出すことはできると思います

グラフを書いてみましょう

得点、平均点、偏差値さえあれば、ExcelのNorm.Distという関数を使って、正規分布のグラフは簡単に描くことができます

それでは、C社通学生の2019年と2021年の本試験の得点と人数分布のグラフを描いて、合格点の予想をしてみましょう

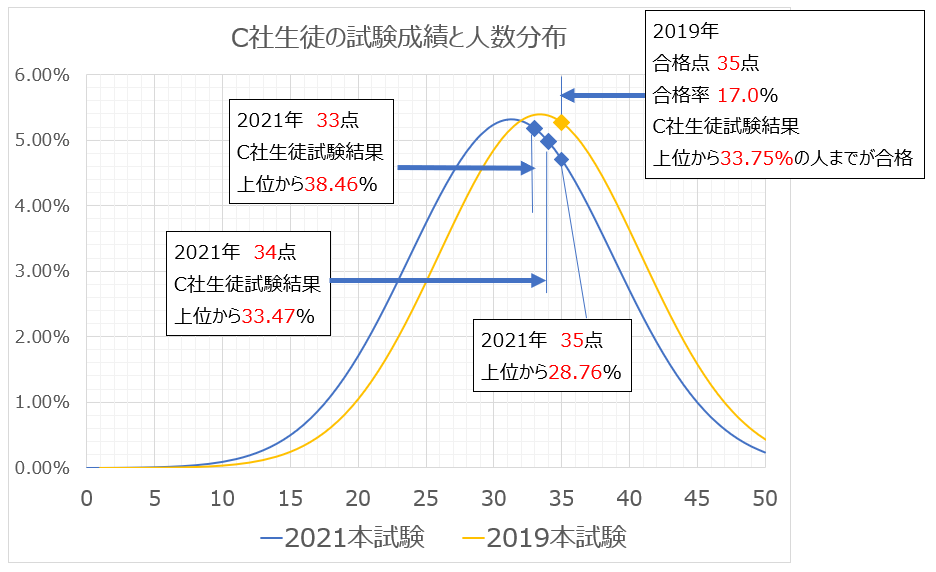
オレンジが2019年本試験、青が2021年の本試験です

さて、分析です。

2019年は、合格点35点 合格率17.0%でした。分布グラフの計算値から、それは、上位33.75%のところにあることがわかりました

では、2021年の本試験は、上位33.75%は、何点のところにあるのでしょうか？

要するに、2019年の合格ラインを、2021年に当てはめると、2021年の33点と34点の間にあります

つまり、2021年の合格率が17%なら、合格ラインは33点と34点の間に入って来ます。ただ、合格率は15ｰ18％で変動しますので、15%なら35点、18%なら33点ぐらいかもしれません

ちなみに2021年の合格点を35点とすると、上位28.76%となり、C社の合格者は大幅に減ってしまうことになり、可能性は低いです

C社の通学生の本試験の平均値が、2019年から2021年に1点以上も下がっているのだから、合格点が35点から34点に1点下がってもおかしくないですよね。35点のままという方が不自然です

まとめ

この分析を読んで、いろいろな疑問がわいてくると思います

そもそも、得点分布はこんなきれいな正規分布のはずはない！とおっしゃる方がいるでしょう。その通りです。こんなきれいな分布にはなりません。ただ、C社の通学生の宅建の学習レベルが同じであることが、この分析の前提です。

そうであるなら、同じ方法で正規分布を描いて両者を相対的に比較するだけなら、統計的には余り問題はありません。絶対値を求めようとすると間違う可能性は高いですね。平均値を用いて合格点を予想してはいけません

◇

いやいや、そうじゃなくて、予備校からは、上位40%が合格って聞いているのに、33.74%が合格って、めちゃくちゃじゃないですか

この分析は、33.74%を求めるためにやった分析ではありません。2019年の合格ラインを元に、2021年の合格ラインを相対的に求めただけです。よって、予備校が言っている40%と数字が異なるのは当然ですし、それが一致する必要はありません

◇

でも、予備校からは、ちゃんとデータに基づいて、合格ライン35点を導き出したと聞いています。なんで、数値が違うのですか？

予備校が、どのようなデータでどうやって分析したかを聞いて見てください。その方法と私のやり方とどちらを信じるかは、あなたにおまかせします

◇

ということで、今回のデータ分析でも合格ラインは、

33点または、34点

になってしまいました

何度もいいますが、自分が34点だから、都合のいいようにデータ分析をしているのだろうと疑っている方も多いと思います

個人的には、どうやって、その疑念を晴らすか方法がわかりません。また、私の分析結果に影響を受けている方がいることを心配しています

できれば、この予測は、競馬の馬券、占いの人生相談、霊能力者の地震予知と思って、ハズレたときはどうぞ、ご勘弁ください。

限られたデータからの分析なので、精度はあまり高くないと思います。仮に当たったとしてもまぐれの可能性が高いです

よろしくお願いいたします

追記：この分析はC社の学習レベルが、2019年と2021年で同一であることを前提にしています。よって、C社の学習レベルが両年で大きく変化した場合、この予測は成り立たなくなります。上には下にも行くということです。そればかりは私には全く情報がありません