宅建の合格点の予測についてまとめをしてみましょう!!
目次
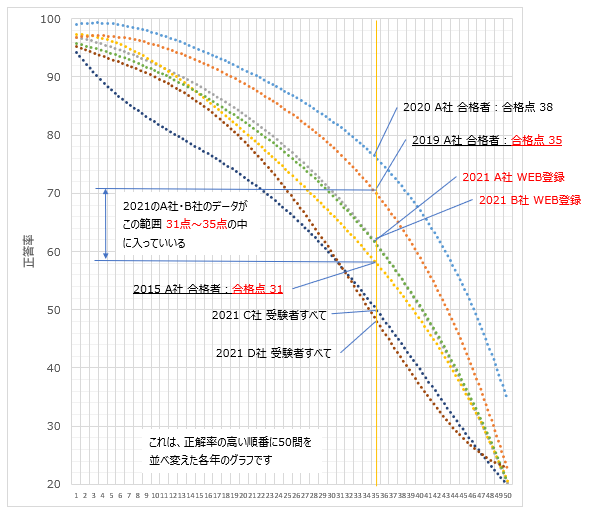
・年ごとのA社合格者の50問の正答率を高い問題順にならべ、近似曲線にする
・曲線は、合格点の順に並ぶことを確認
・その年の本試験後に行われるA社とB社のネット調査の正答率分布曲線と比較することで合格点を予測する
・A社とB社のネット調査のに入力した受験者は不合格者も含まれるのでそれを除くと合格点は少し上昇する
今年(2021年)のA社とB社のネット調査の結果は、過去の31点から35点の間、32点ぐらいのところにあった。ただし、不合格者の得点を除くと曲線は少しだけ上昇するため、33点または、34点と予測した
・A社とB社のネット調査のに入力した受験者の実力分布が不明
・年度によって、受験者全体の実力分布が変動する可能性がある(分布が高ければ合格点があがる、その逆もある)
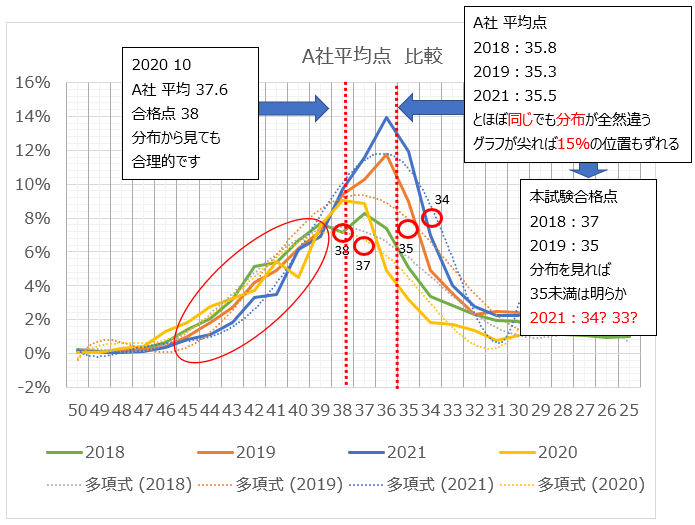
・A社ネット調査の得点と人数分布をグラフ化する
・過去の同様の調査で、平均値がほぼ同じでも、合格点に差がある年を比較(平均値と分布のトンガリ度を比較)
・分布に違いがあり、特に40点以上の高得点者の割合が合格点に影響しており、分布のトンガリ度から、合格点を予測できる
2019年35点の人数分布より、2021年の人数分布はトンガッており、40点以上の人数が極端に少ない。分布全体も低得点側に位置する。このため、合格点は、2019年の35点未満の33点または、34点と予測
それにしても今年(2021年)の分布は尖っていますね。平均点は2018年37点、2019年35点並ですが、トンガッているので、40点以上の得点者がスカスカです。平均値で合格点を考えてはいけない典型例です
・A社とB社のネット調査のに入力した受験者の実力分布が不明
・年度によって、受験者全体の実力分布が変動する可能性がある(分布が高ければ合格点があがる、その逆もある)
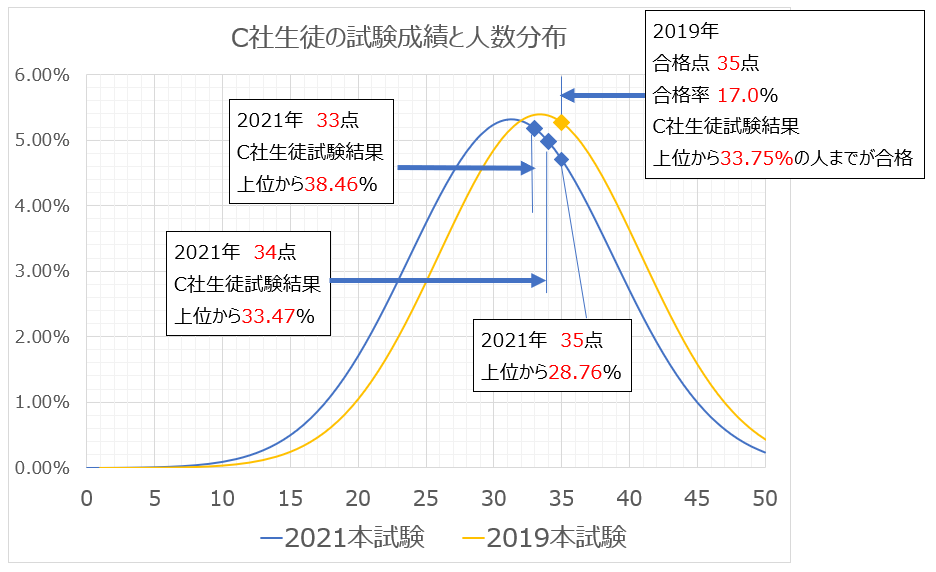
・C社本試験の受験結果の全体はわからないが、得点と人数分布が正規分布になっていると仮定する
・過去の年と今回の得点、平均点、偏差値のデータを入手
・2つの年の正規分布グラフを描画
・過去の年の合格点が上位何%かを計算で求める
・その%以上が今年も合格すると考える
2019年の合格点35点は、上位33.75%の位置にある。よって、2021年も上位33.75%が合格すると考える。正規分布の計算から、35点:28.76%、34点:33.47%、33点:38.46%であった
C社生徒の合格率が、2019年と同様ならば、35点以上では高すぎ、34点以上は合格、33点は合格率次第。よって、33点または、34点が合格
目視でも、2019年35点のプロットの位置をみれば、2021年はどこまで合格できるか予測できます
・C社の受験生の実力が昨年と同様かどうかが不明

私が今年の受験者で34点であることで、分析が公平に行われたか疑いを持たれても仕方がありません。反論があれば、いくらでも行ってください。科学的な分析であれば大歓迎です。いっしょに、宅建の合格点予想の精度を向上させましょう
また、今回の予想は、科学的なアプローチを用いていますが、上記のように数々の懸念事項があるので、どのぐらいの精度で当たるか?と聞かれても答えられません
当たっても、まぐれで当たった。ハズレても、限られたデータの分析だから仕方がなかったとあきらめてほしいです
参考:
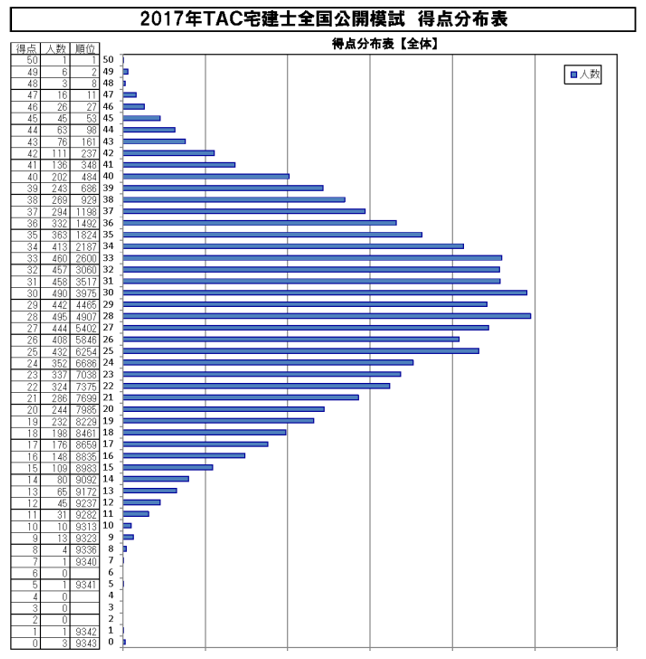
受験生の人数分布が正規分布になるか懸念を持たれている方は、このグラフを御覧ください。TACの全国模試の結果です。平均点29点を中心にきれいな正規分布になっています。母集団が同じと考えられるので、宅建本試験も同じように得点と人数の分布は、正規分布になると思います